前言
最近看到了《python地理空间分析指南》(第二版)中在第 8.5 章节中最短路径的实现,正好有些工程问题需要用这个算法解决,所以往里边钻研了一些。把代码拿来一RUN发现,bug还真不少,各种各样的问题,一通解决下来都快一个月了,不过其实也能理解,这书是14年出的好像,networkx都迭代好几个版本了,在查官网的时候安装了好几个虚拟环境才找出问题所在,好在最后也是成功解决,在这里写一篇文章记录一下这个算法的实现和改良,本文所有代码的运行python版本为3.8 。
数据介绍
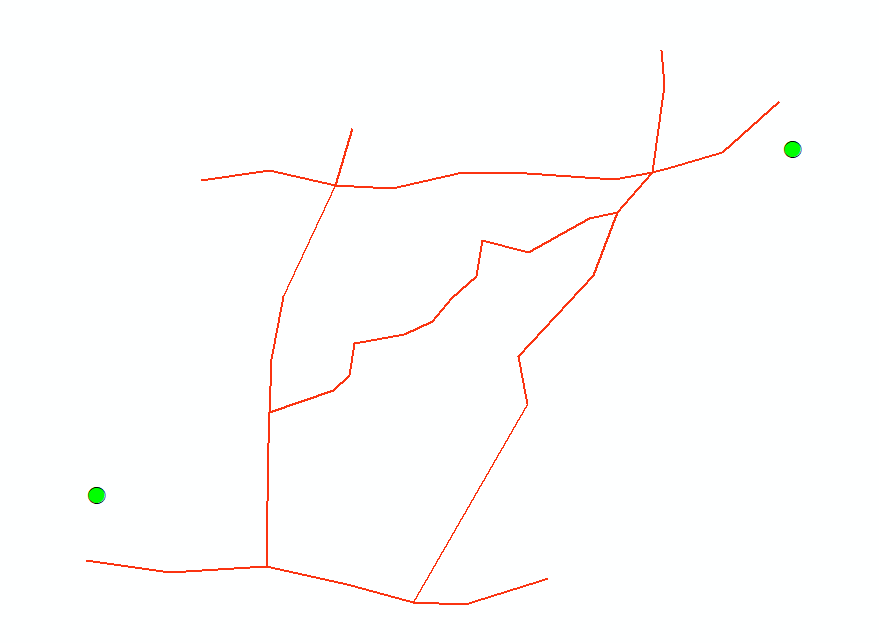
算法主要解决城市中两点的路网最短距离,因此示例数据中给出了起点和终点的Point文件,还给出了简化的路网shapefile polyline,具体见下图。要求找到两点间最短的矢量路线。
设计思想
首先导包:
1
2
3
4
5
|
import networkx as nx
import math
from itertools import tee
import shapefile
from osgeo import ogr
|
用到的函数包括,距离权重计算函数,高效迭代访问函数,其中让我印象深刻的是itertools的tee函数,我是第一次见到原来还能这么迭代坐标对,这给了我很多工程设计上的灵感。原书中这两个函数都有,且目前没有什么bug,这里一块给出:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
def pairwise(iterable):
"""返回可迭代访问的二值元组
s -> (s0,s1), (s1,s2), (s2, s3), ..."""
a, b = tee(iterable)
next(b, None)
return zip(a, b)
def haversine(n0, n1):
x1, y1 = n0
x2, y2 = n1
x_dist = math.radians(x1 - x2)
y_dist = math.radians(y1 - y2)
y1_rad = math.radians(y1)
y2_rad = math.radians(y2)
a = math.sin(y_dist/2)**2 + math.sin(x_dist/2)**2 \
* math.cos(y1_rad) * math.cos(y2_rad)
c = 2 * math.asin(math.sqrt(a))
distance = c * 6371
return distance
|
这里矢量数据的读取,我用的是原书的pyshp包,但不建议用这个包,有许多bug很难在网上找到解决方案,不过好在轻巧,暂且就不改了,然后利用networkx包定义有向图并迭代shapefile的每个节点,得到一个双元组:
1
2
3
4
5
6
|
shp = "road_network.shp"
G = nx.DiGraph()
r = shapefile.Reader(shp)
for s in r.shapes():
for p1, p2 in pairwise(s.points):
G.add_edge(tuple(p1), tuple(p2))
|
接下来这个地方,是需要改动的。先看原文:
1
|
sg = list(nx.connected_component_subgraphs(G.to_undirected()))[0]
|
这里是networkx非常老的版本写法其中connected_component_subgraphs这个函数已经在2.4中被删除了,通过查阅 stackoverflow和networkx 的 github issue前人解决思路,这里改成了如下写法:
1
|
sg = list(G.to_undirected(c) for c in nx.strongly_connected_components (G))[0]
|
这里要注意,光是使用一般的connected_components函数也不行,具体原因我也不清楚,但是报错提示要用 implement 的 connected_components,所以保险起见,就直接用了增强的连通图。
然后是读入起点终点shp点文件,这里和原文写法一致:
1
2
3
|
r = shapefile.Reader(r"start_end.shp")
start = r.shape(0).points[0]
end = r.shape(1).points[0]
|
到这里开始循环迭代计算distance距离。原文中sg.edges_iter和sg.edge[n0][n1]["dist"]写法都已经被弃用,现在需要改成如下:
1
2
3
|
for n0, n1 in sg.edges():
dist = haversine(n0, n1)
sg.edges[n0,n1]["dist"] = dist
|
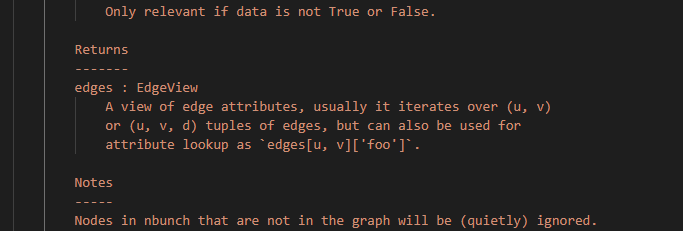
实际上,这里网上目前并没有资料,我也是通过查看原函数中的建议才改正的,读者可以对比原函数和我这里写的,细微的区别得到的结果,往往相差甚远。
接下来一连串的距离迭代比较和networkx最短距离函数调用,基本没有问题,直接用即可:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
nn_start = None
nn_end = None
start_delta = float("inf")
end_delta = float("inf")
for n in sg.nodes():
s_dist = haversine(start, n)
e_dist = haversine(end, n)
if s_dist < start_delta:
nn_start = n
start_delta = s_dist
if e_dist < end_delta:
nn_end = n
end_delta = e_dist
path = nx.shortest_path(sg, source=nn_start, target=nn_end,
weight="dist") #list
|
到了这里,也快结束了,path是一个带有坐标对的list对象,原文中,使用pyshp直接输出,会因为list中坐标对的数字后小数位太长而报错,目前我查看github issue没发现有什么解决办法,因此这里我进行了一些修改,直接使用GDAL的OGR和OSR进行path的list对象以Polyline输出到shapefile,代码也比较常规,算是GDAL的通用写法了。这里给出剩余所有写法:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
multiline = ogr.Geometry(ogr.wkbMultiLineString)
# 构建几何类型:线
line = ogr.Geometry(ogr.wkbLineString)
for point in path:
line.AddPoint(point[0],point[1])
multiline.AddGeometry(line)
wkt = multiline.ExportToWkt()
driver = ogr.GetDriverByName("ESRI Shapefile")
data_source = driver.CreateDataSource("shortest.shp")
srs = osr.SpatialReference()
srs.ImportFromEPSG(4326)
layer = data_source.CreateLayer("shortest", srs, ogr.wkbLineString )
field_name = ogr.FieldDefn("Name", ogr.OFTString)
field_name.SetWidth(14)
layer.CreateField(field_name)
field_name = ogr.FieldDefn("data", ogr.OFTString)
field_name.SetWidth(14)
layer.CreateField(field_name)
feature = ogr.Feature(layer.GetLayerDefn())
feature.SetField("Name", "shortest")
feature.SetField("data", "1.2")
line = ogr.CreateGeometryFromWkt(wkt)
feature.SetGeometry(line)
layer.CreateFeature(feature)
feature = None
data_source = None
|
虽然相比原代码长了一些,但好在它精度高,毕竟直接用了OGR,而且放在工程视角的话,这点长度也不算啥。
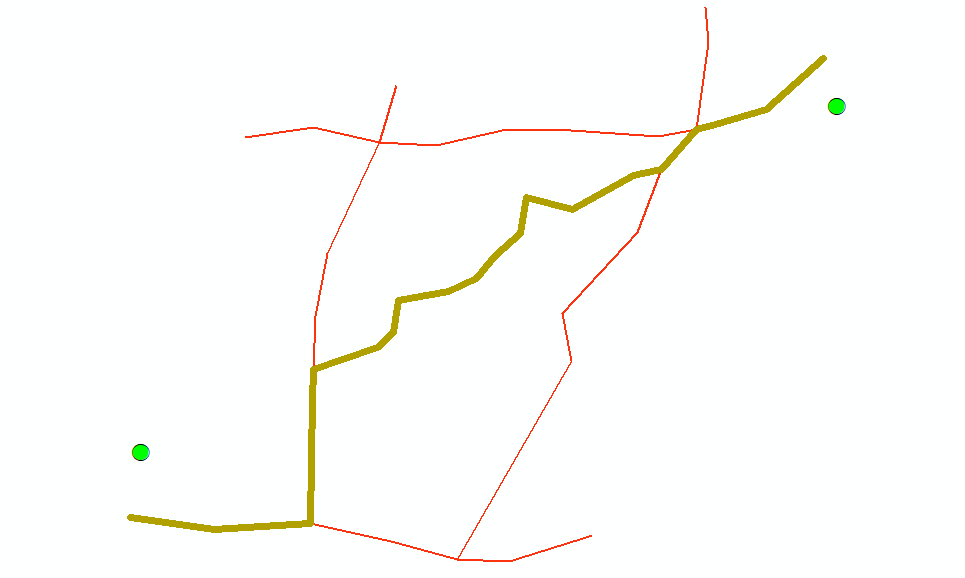
最后放个结果图水水文章长度吧。
后记
虽然代码总共才差不多百行,但是其中版本迭代给原代码造了不少坑,这里写下来留个记录,后续会用到这个算法去做一些更加深入的工程化应用。值得一提的是,这个networkx包目前只能用dijkstra算法,其他如A星、BFS和DFS等算法都没有集成,这算个遗憾。然后如果想了解dijkstra的原理的话,得自己去查了。